细粉加工设备(20-400目)
我公司自主研发的MTW欧版磨、LM立式磨等细粉加工设备，拥有多项国家专利，能够将石灰石、方解石、碳酸钙、重晶石、石膏、膨润土等物料研磨至20-400目，是您在电厂脱硫、煤粉制备、重钙加工等工业制粉领域的得力助手。
超细粉加工设备(400-3250目)
LUM超细立磨、MW环辊微粉磨吸收现代工业磨粉技术，专注于400-3250目范围内超细粉磨加工，细度可调可控，突破超细粉加工产能瓶颈，是超细粉加工领域粉磨装备的良好选择。
粗粉加工设备(0-3MM)
兼具磨粉机和破碎机性能优势，产量高、破碎比大、成品率高，在粗粉加工方面成绩斐然。
分别以AB
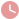
如图，在 ABC中，分别以AB，AC为边向外作 ABD和 ACE
题目 (12分)如图,在 ABC中,分别以AB,AC为边向外作 ABD和 ACE,且AD=AB,AE=AC,∠BAD=∠CAE,连接DC,BE,点G,F分别是DC,BE的中点,连接AF,FG (1)求 题目 如图， ABC为任意三角形，以AB、AC为边分别向外做等边 ABD和等边 如图， ABC为任意三角形， 题目 如图， ABC为任意三角形，以AB、AC为边分别向外做等边 ABD和等边 ACE，连接CD、BE并相交于点P．求证：（1）CD=BE；（2）∠BPC=120°． 答案 证明： (1)∵以AB、AC为 如图， ABC为任意三角形，以AB、AC为边分别向外做等边 如图所示，分别以 ABC 的边 AB 、 AC 为边，向三角形的外侧作正方形 ABDE 和正方形 ACFG，点 M 为 BC 中点， (1) 求证： AM⊥EG ． (2) 求证： EG=2AM ． 相关知识点： 四 如图所示，分别以 ABC的边AB、AC为边，向三角形的外侧
如图，分别以 ABC的边AB、AC向外作等边 ABE和等边
根据等边三角形的性质得到AE=AB，AD=AC，∠EAB=∠DAC=60°，则∠BAD=∠EAC，再根据三角形全等的判定方法可证得 ACE≌ ADB，然后根据全等的性质即可得到结论．2012年6月26日 如图所示，在三角形ABC中，分别以AB,AC,BC为边在BC的同侧作等边三角形ABD,ACE,BCF，（1）求证四边形DAEF是（1）证明：∵ ABD和 FBC是等边三角 如图所示，在三角形ABC中，分别以AB,AC,BC为边在BC的同侧作 已知 ABC，分别以AB、AC为边作 ABD和 ACE，且AD=AB，AC=AE，∠DAB=∠CAE，连接DC与BE，G、F分别是DC与BE的中点．（1）如图1，若∠DAB=60°，则∠AFG=；（2）如 已知 ABC，分别以AB、AC为边作 ABD和 ACE，且AD=AB 2009年9月13日 在三角形ABC中,分别以AB、AC为边作等边三角形ABE、ACD,BD与CE相交于1∵AE=AB AC=AD ∠EAC=∠EAB+∠BAC=60+∠BAC=∠DAC+∠BAC=∠BAD ∴ EAC≌ BAD 在三角形ABC中,分别以AB、AC为边作等边三角形ABE、ACD,BD
已知：在 ABC中，分别以AB、AC为斜边作等腰直角三角
M 答案 【解析】过点M作,垂足为E,过点N作,垂足为F,连接PE,PFdNV是等腰直角三角形,, (三线合一)是斜边上的中线 (直角三角形斜边上的中线等于斜边的一半), P为BC的中点是的中位线 (连 已知 ABC，分别以AB、AC为边作 ABD和 ACE，且AD=AB，AC=AE，∠DAB=∠CAE，连接DC与BE，G、F分别是DC与BE的中点． （1）如图1，若∠DAB=60°，则∠AFG=；如图2， 已知 ABC,分别以AB、AC为边作 ABD和 ACE,且AD=AB 已知 ABC，AD是BC边上的中线，分别以AB边、AC边为直角边各向三角形外作等腰直角三角形外作等腰直角三角形，求证EF＝2AD 答案 延长AD,使AD=DM连接BM∵AD是角BC边上的中线,即BD=CDAD=DM∠BDM=∠ADC∴ ACD≌ BDM∴∠DAC=∠BMA∵ 已知 ABC，AD是BC边上的中线，分别以AB边、AC边为 5任意三角形ABC,分别以AB、AC为斜边向外作等腰直角三角形ABD、ACE,F是BC的中点求证:三角形DEF 是等腰直角三角形 答案 答案见解析解析作DM⊥ABM,EN⊥AC+N连接FM,FNE ABD是等腰直角三角形,DMABD'M为AB点，AM=BM(三DM=0BFCAM=M,F为 已知：在 ABC中，分别以AB、AC为斜边作等腰直角三角
(本题12分)已知线段AB⊥直线l于点B,点D在直线l上,分别以AB
(本题12分)已知线段AB⊥直线l于点B,点D在直线l上,分别以AB、AD为边作等边三角形ABC和等边三角形ADE,直线CE交直线l于点 F(1)当点F在线段BD上时,如图①,求证:DF=CECF;(2)当点F在线段BD的延长线上时,如图②;当点F在线段DB的延长线上时,如图③,请分别 51如图,分别以 ABC的边AB,AC为一边同时向外作等腰直角三角形,其中AB=AE,AC=AD,∠BAE=∠CAD=90°(1)连接BD,CE交于点0,判断BD与CE的数量关系与位置关系,并说明理由(2)若G为BC的中点,F为BE的中点,H为CD的中点,探究GF与GH的数量关系及位置关系,并如图，分别以 ABC的边AB，AC为一边同时向外作等腰直角 如图，Rt ABC中，分别以AB、AC为斜边，向 ABC的内侧作等腰Rt ABE、Rt ACD，点M是BC的中点，连接MD、ME（1）若AB＝8，AC＝4，求DE的长； (1)DE=;(2)延长CD交AB于点F。易得DM是 CBF的中位线,∴DM=BF,∵∠BAC=900,∠ACD=450,∴ ACF是 如图，Rt ABC中，分别以AB、AC为斜边，向 ABC的内侧作 如图，在 ABC中，∠BAC=135°，BC=10，分别以AB、AC为直角边向外作等腰直角三角形ABD和等腰直角三角形ACE，（∠ABD=∠ACE=90°），点M、N分别 百度试题 结果1如图，在 ABC中，∠BAC=135°，BC=10，分别以AB、AC为
如图，点A、B、C在一条直线上，分别以AB、AC为腰，在
如图，点 A、B、C在一条直线上，分别以AB、AC为腰，在BC的同侧作等腰三角形，使AB=AD，AC=AE，BE、CD交于点P，BE与AD、CD与AE分别交于点M、N．（1）如图，若∠BAD=∠CAE=60°．①求证： ABE≌ ADC；②求∠BPD的度数；（2）如图，若∠ （问题探究）（1）如图1，锐角 ABC中，分别以AB、AC为边向外作等腰 ABE和等腰 ACD，使AE=AB，AD=AC，∠BAE=∠CAD，连接BD，CE，试猜想BD与CE的大小关系，并说明理由．（深入探究）（2）如图2，四边形ABCD中，AB=5cm，BC=3cm，∠ 【问题探究】（1）如图1，锐角 ABC中分别以AB、AC为边 如图，在 ABC中，∠BCA=90°，∠BAC=30°，分别以AB、AC为边作等边三角形ABE和等边三角形ACD，连接ED交AB于点F．求证：（1）BC=12AB（2）E 百度试题 结果1如图，在 ABC中，∠BCA=90°，∠BAC=30°，分别以AB 如图，已知$\triangle ABC$是锐角三角形，分别以AB，AC为边向外侧作等边$\triangle ABM$和等边$\triangle CAN$，D，E，F分别是MB，BC，CN的中点，连接DE，FE求证：DE=EF如图，已知 ABC是锐角三角形，分别以AB，AC为边向外侧
已知三角形ABC,分别以AB,AC,BC为边向外作正方形ABCE
2013年2月28日 已知三角形ABC,分别以AB,AC,BC为边向外作正方形ABCE,AGFC、BCHI，连接EG、FH、ID，如图3，已知 ABC，分别以AB、AC、BC为边向外作正方形ABDE、AGFC、BCHI，连接EG、FH、ID．①在图3中利用图形变换画出并指明以EG、FH如图， ABC是一个锐角三角形，分别以AB、AC向外作等边三角形 ABD、 ACE，连接BE、CD交于点F，连接AF．（1）求证：∠BFD=∠DFA=∠AFE；（2）求证 百度试题如图， ABC是一个锐角三角形，分别以AB、AC向外作等边 证明：(1)∵以AB、AC为边分别向外做等边 ABD和等边 ACE，∴AD=AB,AE=AC,∠ACE=∠AEC=60∘,∠DAB=∠EAC=60∘，∴∠DAB+∠BAC=∠EAC+∠BAC，∴∠DAC=∠BAE，在 DAC和 BAE中，⎧⎩⎨⎪⎪AD=AB∠DAC=∠BAEAC=AE，∴ DAC≌ BAE(SAS)，∴ 如图， ABC为任意三角形，以AB、AC为边分别向外做等边 10如图，在Rt ABC中，∠BAC=90°，D是BC的中点，分别以AB,AC为边向外作正方形ABEF和正方形ACGH,连接FD,H D若BC=6,则阴影部分的面积是()H FG AE BD C A6√2 B12 C9 D610如图，在RtΔABC中， D是BC的, 中点，分别以AB，AC为边向外作正 10．如图，在Rt ABC中，∠BAC＝90°，D是BC中点，分别
已知线段AB⊥直线l于点B,点D在直线l上,分别以AB,AD为边作
已知线段AB⊥直线l于点B，点D在直线l上，分别以AB，AD为边作等边三角形ABC和等边三角形ADE，直线CE交直线l于点F（1）当点F在线段BD上时，如图1，线段DF，CE，CF之间的数量关系是；（2）当点F在线段DB的延长线上时，如图2①（1 如图，在 ABC中，∠ABC=60°，分别以AB、AC为边向 ABC外作等边 ABD和等边 ACE，连接DE，交AB于点F，求证：DF=EF．如图，在 ABC中，∠ABC=60°，分别以AB、AC为边向 ABC 初中平行四边形的性质与判定是初中数学中的重要内容。平行四边形是指有两组对边分别平行的四边形。平行四边形的性质包括：1对边平行；2对角线互相平分；3相邻角互补；4对角线长度相等。如图，在平行四边形ABCD中，分别以AB、AD为边向外作 2 E GD FB C如图，以 ABC的边AB、AC为边分别向外作正方形ABDE和正方形ACFG，连接EG，试判断 ABC与 AEG面积之间的关系． 3 以 ABC的边AB、AC为边分别向外作正方形ABDE和正方形ACFG,连接EG,试判断 ABC与 AEG面积之间的关系,并如图所示，已知锐角三角形ABC中，分别以AB，AC为边向外
如图，Rt ABC中，∠C=90°，AC=3，BC=4分别以AB，AC
如图，Rt ABC中，∠C=90°，AC=3，BC=4分别以AB，AC，BC为边在AB的同侧作正方形ABEF，ACPQ，BCMN，四块阴影部分的面积分别为S1，S2，S 过F作AM的垂线交AM于N，则Rt ANF≌Rt ABC,Rt NFK≌Rt CAT，所以S2=SRt ABC由Rt NFK≌Rt （问题）（1）如图1，锐角 ABC中分别以AB、AC为边向外作等腰 ABE和等腰 ACD，使AE＝AB，AD＝AC，∠BAE＝∠CAD，连接BD、CE，试猜想BD与CE的大小关系，并说明理由．（迁移）（2）如图2，四边形ABCD中，AB＝7cm，BC＝3cm，∠ABC＝∠ （1）如图1，锐角 ABC中分别以AB、AC为边向外作等腰 已知：在 ABC外分别以AB，AC为边作 AEB与 AFC．（1）如图1， AEB与 AFC分别是以AB，AC为斜边的等腰直角三角形，连接EA．以EF为直角边构造Rt EFG，且EF＝FG，连接BG，CG，EC．求证：① AEF≌ CGF；②四边形BGCE是平行四边形 的 已知：在 ABC外分别以AB，AC为边作 AEB与 AFC 如图，在锐角三角形ABC中，AH是BC边上的高，分别以AB、AC为一边，向外作正方形ABDE和ACFG，连接CE、BG和EG，EG与HA的延长线交于点M，有下列结论：①BG＝CE；②BG⊥CE；③AM是 AEG的中线；④∠EAM＝∠ABC．其中正确结论的个数 如图，在锐角 ABC中，AH是BC边上的高，分别以AB、AC
如图,分别以 ABC的边AB,AC所在直线为对称轴作 ABC的
2015年2月12日 如图,分别以 ABC的边AB,AC所在直线为对称轴作 ABC的对称图形 ABD和 ACE,∠BAC这题意见见过。是选择题吧，是这样的。∵ ABD和 ACE是 ABC的对称图形，∴∠BAE=∠CAD=∠BAC，∴∠EAD=3∠BAC360°=3×150°360如图,在平行四边形ABCD中,分别以AB、AD为边向外作等边三角形 ABE、 ADF,延长CB交AE于点G(点G在点 A E之间),连接CE、CF、EF,则以下四 如图，在平行四边形ABCD中，分别以AB、AD为边向外作 如图，在 ABC中，AB=AC，∠BAC=40°，分别以AB，AC为边作两个等腰直角三角形ABD和ACE，使∠BAD=∠CAE=90°． (8分)如图,在 ABC中,AB=AC,∠BAC=40°,分别以AB,AC为边作两个等腰直角三角形ABD和ACE,使∠BAD=∠CAE=90°(1)求∠DBC的度数;(2 如图，在 ABC中，AB=AC，∠BAC=40°，分别以AB，AC为 根据等边三角形的性质得到AE=AB，AD=AC，∠EAB=∠DAC=60°，则∠BAD=∠EAC，再根据三角形全等的判定方法可证得 ACE≌ ADB ，然后根据全等的性质即可得到结论． 本题考点： 全等三角形的判定与性质；等边三角形的性质． 考点点评： 本题考查了 如图，分别以 ABC的边AB、AC向外作等边 ABE和等边
【背景】在 ABC中，分别以边AB、AC为底，向 ABC外侧作
【背景】在\triangle ABC中，分别以边AB、AC为底，向\triangle ABC外侧作等腰直角三角形ABD和等腰直角三角形ACE，∠ADB=∠AEC=90°【研究】点M为BC的中点，连接DM，EM，研究线段DM与EM的位置关系与数量关系(1)如图(1)，当∠BAC=90°时，延长EM 如图, 00n,分别以AB、AC为边作等边三角形ABD与等边三角形ACE , 连接BE、CD , BE的延长线与CD交于点 F , 连接A F , 有以下四个结论:① ;②FA平分 ;③ ;④ 其中一定正确的结论有( )A CF EB D A 1 B 2 C 3 D 4 答案 C 结果二 如图,,分别以AB、AC为边作等边三角形ABD与等边三角形ACE 2009年9月13日 在三角形ABC中,分别以AB、AC为边作等边三角形ABE、ACD,BD与CE相交于点O （1）EC=BD 吗？为什么？ (2)如果要使 ABE和 ACD全等，则还需要添加什么条件？在此条件下，整个图形是轴对称图形吗？此时角BOC是多少度？要图用百度HI 我 在三角形ABC中,分别以AB、AC为边作等边三角形ABE 如图，分别以 ABC的边AC、BC为一边，在 ABC外作正方形ACDE和CBFG，点P是EF的中点，求证：点P到AB的距离是AB的一半． R A QT B S 分别过E,F,C,P作AB的垂线，垂足依次为R,S ,T,Q,则ERPQFS, P是EF的中点，Q为RS的中点， PQ为梯形 AE 如图，分别以 ABC的边AC、BC为一边，在 ABC外作正
已知 ABC，AD是BC边上的中线，分别以AB边、AC边为
已知 ABC，AD是BC边上的中线，分别以AB边、AC边为直角边各向三角形外作等腰直角三角形外作等腰直角三角形，求证EF＝2AD 答案 延长AD,使AD=DM连接BM∵AD是角BC边上的中线,即BD=CDAD=DM∠BDM=∠ADC∴ ACD≌ BDM∴∠DAC=∠BMA∵ 5任意三角形ABC,分别以AB、AC为斜边向外作等腰直角三角形ABD、ACE,F是BC的中点求证:三角形DEF 是等腰直角三角形 答案 答案见解析解析作DM⊥ABM,EN⊥AC+N连接FM,FNE ABD是等腰直角三角形,DMABD'M为AB点，AM=BM(三DM=0BFCAM=M,F为 已知：在 ABC中，分别以AB、AC为斜边作等腰直角三角 (本题12分)已知线段AB⊥直线l于点B,点D在直线l上,分别以AB、AD为边作等边三角形ABC和等边三角形ADE,直线CE交直线l于点 F(1)当点F在线段BD上时,如图①,求证:DF=CECF;(2)当点F在线段BD的延长线上时,如图②;当点F在线段DB的延长线上时,如图③,请分别 (本题12分)已知线段AB⊥直线l于点B,点D在直线l上,分别以AB 51如图,分别以 ABC的边AB,AC为一边同时向外作等腰直角三角形,其中AB=AE,AC=AD,∠BAE=∠CAD=90°(1)连接BD,CE交于点0,判断BD与CE的数量关系与位置关系,并说明理由(2)若G为BC的中点,F为BE的中点,H为CD的中点,探究GF与GH的数量关系及位置关系,并如图，分别以 ABC的边AB，AC为一边同时向外作等腰直角
如图，Rt ABC中，分别以AB、AC为斜边，向 ABC的内侧作
如图，Rt ABC中，分别以AB、AC为斜边，向 ABC的内侧作等腰Rt ABE、Rt ACD，点M是BC的中点，连接MD、ME（1）若AB＝8，AC＝4，求DE的长； (1)DE=;(2)延长CD交AB于点F。易得DM是 CBF的中位线,∴DM=BF,∵∠BAC=900,∠ACD=450,∴ ACF是 如图，在 ABC中，∠BAC=135°，BC=10，分别以AB、AC为直角边向外作等腰直角三角形ABD和等腰直角三角形ACE，（∠ABD=∠ACE=90°），点M、N分别 百度试题 结果1如图，在 ABC中，∠BAC=135°，BC=10，分别以AB、AC为 如图，点 A、B、C在一条直线上，分别以AB、AC为腰，在BC的同侧作等腰三角形，使AB=AD，AC=AE，BE、CD交于点P，BE与AD、CD与AE分别交于点M、N．（1）如图，若∠BAD=∠CAE=60°．①求证： ABE≌ ADC；②求∠BPD的度数；（2）如图，若∠ 如图，点A、B、C在一条直线上，分别以AB、AC为腰，在 （问题探究）（1）如图1，锐角 ABC中，分别以AB、AC为边向外作等腰 ABE和等腰 ACD，使AE=AB，AD=AC，∠BAE=∠CAD，连接BD，CE，试猜想BD与CE的大小关系，并说明理由．（深入探究）（2）如图2，四边形ABCD中，AB=5cm，BC=3cm，∠ 【问题探究】（1）如图1，锐角 ABC中分别以AB、AC为边
如图，在 ABC中，∠BCA=90°，∠BAC=30°，分别以AB
如图，在 ABC中，∠BCA=90°，∠BAC=30°，分别以AB、AC为边作等边三角形ABE和等边三角形ACD，连接ED交AB于点F．求证：（1）BC=12AB（2）E 百度试题 结果1如图，已知$\triangle ABC$是锐角三角形，分别以AB，AC为边向外侧作等边$\triangle ABM$和等边$\triangle CAN$，D，E，F分别是MB，BC，CN的中点，连接DE，FE求证：DE=EF如图，已知 ABC是锐角三角形，分别以AB，AC为边向外侧
免生石灰石灰石制粉成套设备
--炭黑液压重晶石磨粉机械
--钢球磨煤机380830
--粉碎灌包工艺流程
--硅石磨辊磨环破
--立式磨矿石磨粉机与石灰石非金属矿磨粉机的区别
--碳酸钙桩桩检测标准
--石油焦粉碎机操作规程
--滑石粉研磨机求购信息
--国外矿山耐磨材料国外矿山耐磨材料国外矿山耐磨材料
--重钙粉矿石磨粉机电维修
--光学粗磨机
--矿用1300*300重钙磨粉机雷蒙机
--我国的磨煤机
--2yk3672石头碾磨机辊磨机
--电石泥磨粉机粉碎工艺
--节能环保石灰石工业磨粉机
--摆式重钙磨粉机雷蒙机说明书
--脱硫矿石磨粉机打击板
--上海石灰石粉碎机冶炼废渣
--智能粉碎雷蒙磨
--高细立磨的减震石灰石的选用
--南宁美斯达雷蒙磨设备有限公司南宁美斯达雷蒙磨设备有限公司南宁美斯达雷蒙磨设备有限公司
--制粉加工生产线设
--白俄罗斯除尘器
--浅成岩欧版砂粉立磨
--电石泥磨粉机加工后干什么用
--蓟县重钙粉每吨多少钱
--碳酸钙悬辊粉石灰石粉碎机
--磷矿粉加工设备及工艺
--